L'essenziale del linguaggio Java per realizzare l'insieme di Mandelbrot e di Julia.
Capitolo 3:
Il primo Insieme di Mandelbrot
Cominciamo un nuovo applet ripetendo la procedura vista prima, questo terzo applet lo chiameremo MandPicture1.
Prima di cominciare il nuovo listato vi devo dire qualcosa sulle moltiplicazioni e sulle somme tra i numeri complessi,(chi li conosce già può andare direttamente al listato qui sotto) non allarmatevi non sono molto più complessi delle solite operazioni e poi a noi basta saper moltiplicare e sommare, perchè la sottrazione e la divisione non ci serve.
Per prima cosa un numero complesso è composto da una parte reale ed una immaginaria, anche qui non c'è da preoccuparsi anche la parte immaginaria è composta dai soliti numeri, ma cosa hanno di speciale questi numeri?
Questi numeri specificano un punto su di un piano, mentre i numeri reali lo specificano solo su una linea, se voglio trovare un punto su di una linea mi basta scegliere un numero, ad esempio se dico -2 indico un punto che si trova 2 unità prima dello zero, mentre se dico 1,25 specifico un punto che si trova a 1,25 unità dopo lo zero.
I reali però non mi permettono di specificare un punto su di un piano, mentre con i numeri complessi che inizialmente furono usati per la risoluzione delle equazioni di terzo e quarto grado da parte di Tartaglia (un matematico del XVI secolo), lo posso fare, perchè essendo composti da due numeri, possono essere utilizzati abbinandoli ai punti del piano "cartesiano" (Da René Descartes, filosofo e matematico francese, italianizzato in Renato Cartesio)che è determinato da 2 numeri uno per le ascisse e uno per le ordinate
mentre per lo spazio tridimensionale ce ne vogliono 3 e per quello quadrimensionale ne servono 4.
I numeri per meneggiare lo spazio tridimensionale, si chiamano quaternioni sono rappresentati in questo modo ( w + xi + yj + zk) , dove w , x , y , z sono nemeri reali e (i , j , k) sono le unità immaginarie,
I quaternioni sono una estensione dei numeri complessi, come quest'ultimi sono una estensione dei numeri reali.
Ma ora torniamo al piano cartesiano
Tutti conosciamo il piano cartesiano perché ne abbiamo usato uno simile per giocare.Perciò "b4" significava, che il quadretto specificato si trovava all'incrocio tra la seconda riga, la "b è la seconda lettera dell'alfabeto" e la quarta colonna.
Con i numeri complessi si usa lo stesso sistema, con la differenza che al posto di una lettera e un numero usiamo due numeri per identificare tutti i punti sul piano, anche perchè le lettere dell'alfabeto sono veramente poche mentre i punti sul piano sono infiniti.
Per distingure le righe dalle colonne il numero complesso è l'ideale perchè come abbiamo visto è composto da due parti.
Il piano complesso è diviso in 4 quadranti con lo zero nel centro, ne vedete un esempio nell'immagine qui a sinistra, se guardate le due righe verdi potete vedere che il punto che le unisce è posto 2 unità a destra e 3 in alto dal punto zero centrale, questi punti sono le coordinate cartesiane e vengono rapprentati con i numeri complessi in questo modo, per esempio il punto verde si scrive 2 +3i il numero 2 è la parte reale mentre il 3 rappresenta la parte immaginaria, i punti sinistra e a destra dello zero sulla riga orrizzontale o "ascissa in matematica", sono la parte reale del numero complesso, mentre quelli a nord e a sud dello zero, cioè la colonna verticale, " ordinata in matematica" rappresentano la sua parte immaginaria .
Ancora una cosa i punti alla destra dello zero, sono la parte positiva, mentre quelli a sinistra sono la parte negativa delle ascisse.
Per le ordinate abbiamo a nord quelli positivi, mentre a sud abbiamo i negativi, ecco un altro esempio -3 +1i sempre nell'immagine rappresenta il punto rosso, nota che quando il numero reale è positivo non si mette il segno "+" davanti al numero, mentre quando è negativo naturalmente si deve mettere, con la parte immaginaria normalmente si mette sia quando è positivo"+" sia quando è negativo "-" .
La somma tra due numeri complessi è molto simile alla somma odinaria, basta sommare separatamente le 2 parti reali e le due parti immaginarie,
| 3 | +13i |
| 2 | +3i |
| = | |
| 5 | +16i |
Ecco un esempio.
Come vedi vengono sommati i numeri separatamente senza tener conto del riporto
| . | 1 | +3i |
| x | 3 | +3i |
| = | ||
| . | 3 | +9i |
| 3 | 9 | . |
| _6 | +12i | . |
Il primo modo è questo a sinistra è uguale a quello appreso alle elementari, il prodotto tra due numeri complessi (Z= 1 +3i) e (w = 3+3i), è del tutto identico alla solita moltiplicazione, tranne l'ultima riga, quella del risultato, per un motivo che sarebbe un poco lungo da spiegare, la parte immaginaria del numero cambia di segno (il più diventa meno e viceversa) e viene sommata alla parte reale, perciò "+9i" diventa "-9i" e viene sommato a "3 che è la parte reale" a questo punto diventa "-9 +3 = -6" ed il "9i" viene eliminato, mentre la nuova parte immaginaria diventa la normale somma di "9+3 = 12i"
Perciò il prodotto di Z per W = "-6 +12i"
Avremo (ac-bd) +i(ad+bc) avremo ancora (1*3-3*3 = 3-9 = -6) per la parte reale, e (1*3+3*3 = 3+9 = 12)per la parte immaginaria.
come vedi ancora più semplice ed è quello che useremo noi.
Il terzo metodo è quello geometrico, noi non lo useremo, ma ne mostro ugualmete un breve esempio, questo metodo invece delle coordinate cartesiane usa quelle polari, un esempio di coordinata polare è "ρ5 θ" dove "ρ5" è il raggio, mentre "θ" è un valore angolare,
A sinistra il numero complesso "3 +4i" in coordinate cartesiane corrisponderebbe in coordinate polari a"ρ5 54°" perchè ρ5 è il raggio (la linea rossa) ossia la radice quadrata di 3² + 4² = 25
mentre 54° e la misura dell'angolo in gradi misurato a partire dalla linea orizzontale alla destra dello zero fino al punto d'incontro con il raggio (r)"
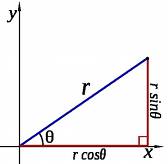Come vedi la parte reale del numero complesso e data da raggio per il coseno dell'angolo "θ" e la parte immaginaria corrisponde a raggio per seno di "θ"
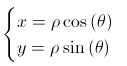
Perciò conoscendo l'angolo "θ" avremo la parte reale X = (5 per coseno di θ") e la parte immaginaria Y= ( 5 per seno di θ)
Il prodotto tra due numeri complessi è molto più facile usando le coordinate polari, perché basta moltiplicare i due raggi(moduli) per avere il nuovo modulo e addizionare i due angoli (fasi o argomenti) per ottenere il nuovo argomento(angolo);
ad esempio per moltiplicare due num.complessi U e V con U avente raggio =3 e angolo =1.2 e V con raggio =5 e angolo =0.8 il prodotto avrà raggio =3*5 = 15 e angolo 1.2+0.8 = 2
mentre se dovessimo elevare a n=3 il numero complesso U con un raggio(modulo)= 2 e angolo (argomento= 0.5) avremmo come risultato modulo 2³= 8 e argomento = 0.5+0.5+0.5= 3*0.5 =1.5
L'inconveniente delle coordinate polari è che occore conoscere il valore dell'angolo e per ottenerlo bisogna ricorrere alla funzione trigonometrica arcotangente oltre alle funzioni seno e coseno e ciò rallenta l'esecuzione del programma.
Potete selezionare il testo, copiarlo e incollarlo all'interno dell'applet MandPicture1 che avevate aperto, eseguitelo dovreste vedere una immagine simile a questa sotto
I punti colorati in nero appartengono all'insieme di Mandelbrot
Vediamo un attimo la formula dell'insieme di Mandelbrot che è Z² +c dove Z e c sono due numeri complessi, Z² è uguale a Z*Z ed abbiamo già visto come moltiplicare e addizionare due numeri complessi.
Ma la cosa che ha permesso di mettere in luce i risultati di questa formula quando è sottoposta a una determinata condizione, è stato l'avvento del computer, che con la sua velocità di calcolo ha permesso di reiterare questa formula per migliaia di volte in un tempo brevissimo, tutti questi calcoli abbinati ad un algoritmo adatto hanno permesso di creare una immagine con una caratteristca molto particolare, quando viene ingrandita la zona nelle vicinanze del bordo nero, mostra dei particolari dalle forme esteticamente molto belle e che nascondono al loro interno delle immagini molto simili al disegno originale, a loro volta queste copie se ingrandite rivelano altre copie con all'interno altre copie in un ciclo senza fine, limitato solo dalla potenza dell'elaboratore, gli ingrandimenti possono raggiungere tranquillamente molte decine di milioni di volte l'originale, ne vedremo alcuni nel prossimo capitolo.
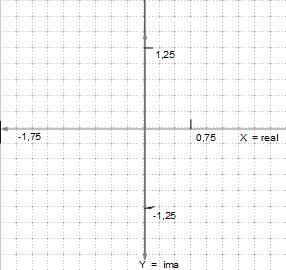Vediamo ora i punti del piano complesso interessati dalla formula.La formula dell'insieme di Mandelbrot prende in considerazione solo una porzione abbastanza piccola del piano, vale a dire da -1.75 fino a 0.75 per le ascisse ossia la parte reale dei numeri complessi e da -1,25 fino a 1,25 per le ordinate cioè la parte immaginaria, abbiamo perciò una superfice del piano uguale a 2,5 x 2,5.
A questo punto dobbiamo mettere in relazione questa piccola superfice con la superfice del monitor che useremo per vedere il disegno.
Se consideriamo che il nostro esempio è formato da 500 x 500 pixel, la nostra formula verrà ripetuta almeno 250.000 volte, ma dato che per colorare un singolo pixel la ripeteremo ancora almeno una decina di volte in media, ne segue che arriveremo facilmete a 2.500.000 di volte.
Abbiamo visto che ogni ad punto del piano complesso in esame, corrisponde un pixel sul monitor, Ma eseguire la formula per ogni punto non basta, serve anche una regola per stabilire se e quando accendere il pixel relativo al punto del piano preso in esame, questa regola è molto semplice; se il valore assoluto del risutato ottenuto con l'applicazione della formula e inferiore a 2 allora quel punto del piano preso in esame
appartiene all'insieme di mandelbrot.
Ora vediamo cos'è il valore assoluto di un numero complesso: - Abbiamo visto che il numero complesso è formato da una parte reale ed una immaginaria, ebbene il suo valore assoluto è dato dalla radice quadrata della somma dei quadrati della parte reale con la parte immaginaria.
A dirlo sembra un scioglilingua, ma in effeti è molto semplice.
Ad esempio come vedi dall'immagine, se la parte reale è 3 e la parte immaginaria è 4 il suo valore assoluto sarà la radice quadrata di (3x3 + 4x4 = 25)cioè √ 25 = 5.
Praticamente il valore assoluto è l'ipotenusa del triangolo formato con i 2 lati corrispondenti alle 2 componenti del numero complesso
A questo punto dobbiamo solo stabilire quante volte dobbiamo ripetere l'algoritmo che esegue la formula, per stabilire se il punto del piano in esame ha un modulo inferiore a |2|.
Il problema è che quando si usa questa formula, alcuni numeri complessi che corrispondono ai dintorni dell'origine del piano C. hanno un comportamento strano, praticamente si mettono a saltellare da un punto all'altro del piano senza mai riuscire a raggiungere il valore assoluto o modulo |2|, quei numeri che non superano la barriera del numero 2 sono appunto quelli che verrano colorati in nero perchè appartengono all'imsieme di mandelbrot, mentre tutti quelli che riescono a farcela verrano colorati in base al numero di saltelli che hanno fatto prima di riuscire a superarla.
Decidere quanti cicli (saltelli) dobbiamo lasciar fare al programma per decidere se è un numero dell'insieme di mandelbrot, dipende dal numero degli ingrandimenti che si vogliono ottenere, per pochi ingrandimenti bastano pochi cicli, ma per forti ingrandimenti, ne possono servire centinaia.
Nel prossimo capitolo vedremo come ingrandire i punti più interessanti.